Renkli kareler ve güneş tutulmaları
Makale, Ulusal Çocuk Fonu bursluları olan ortaokul öğrencileri için derslerimi anlatıyor. Vakıf, özellikle üstün zekalı çocukları ve gençleri (ilkokul XNUMX. sınıftan liseye kadar) araştırmakta ve seçilen öğrencilere “burs” vermektedir. Bununla birlikte, hiçbir şekilde nakit çekmekten değil, kural olarak uzun yıllar boyunca yeteneğin geliştirilmesine yönelik kapsamlı bakımdan oluşurlar. Bu tür birçok projenin aksine, tanınmış bilim adamları, kültürel figürler, önde gelen hümanistler ve diğer bilge kişiler ve ayrıca bazı politikacılar Vakfın vesayetini ciddiye alıyorlar.
Vakfın faaliyetleri, sanat da dahil olmak üzere spor dışında, temel okul dersleri olan tüm disiplinleri kapsar. Fon, 1983 yılında o zamanki gerçekliğe bir panzehir olarak kuruldu. Herkes fona başvurabilir (genellikle bir okul aracılığıyla, tercihen okul yılının bitiminden önce), ancak elbette belirli bir eleme, belirli bir yeterlilik prosedürü vardır.
Daha önce de belirttiğim gibi, makale, Mart 2016'da, III lisedeki 24. ortaokulda, özellikle Gdynia'daki ustalık derslerime dayanmaktadır. Donanma. Uzun yıllardır bu seminerler, Vakfın himayesinde, olağanüstü karizma ve yüksek entelektüel seviyeli bir öğretmen olan Wojciech Thomalczyk tarafından düzenleniyor. 2008 yılında, Polonya'da Pedagoji Profesörü unvanını alan ilk ona girdi (uzun yıllar önce kanunla sağlanan). “Eğitim dünyanın eksenidir” ifadesinde biraz abartı vardır.
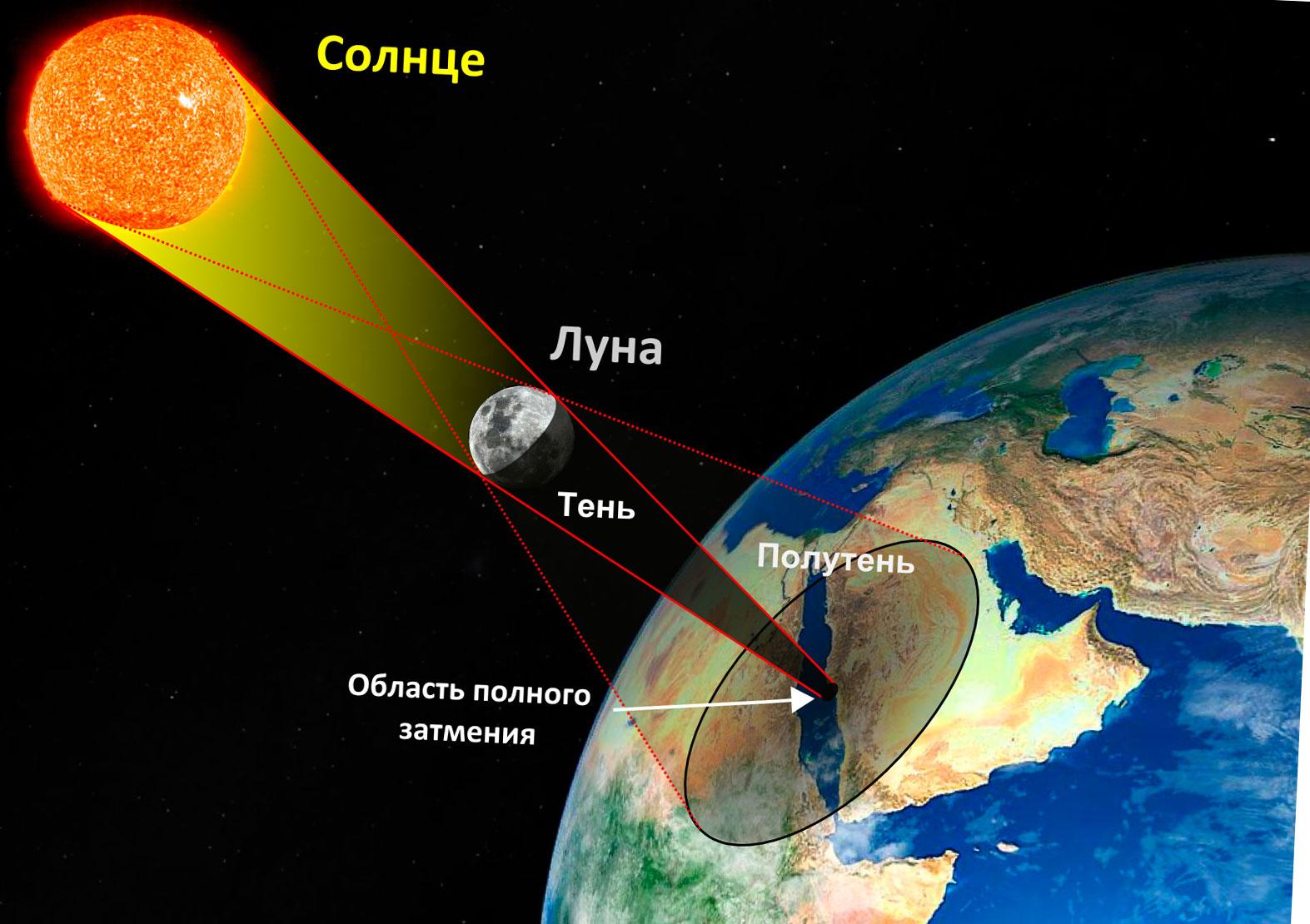
ve ay her zaman büyüleyici - o zaman her şeyin hareket halinde olduğu, santimetre ve saniyelerle ölçülen devasa bir uzayda küçük bir gezegende yaşadığımızı hissedebilirsiniz. Hatta zaman perspektifi beni biraz korkutuyor. Bugünün Varşova bölgesinden görülebilen bir sonraki tam tutulmanın ... 2681'de olacağını öğreniyoruz. Bakalım kim görecek? Gökyüzümüzdeki Güneş ve Ay'ın görünen boyutları hemen hemen aynıdır - tutulmaların bu kadar kısa ve muhteşem olmasının nedeni budur. Yüzyıllar boyunca, bu kısa dakikalar astronomların güneş koronasını görmeleri için yeterli olmalı. Yılda iki kez olmaları garip ama bu sadece Dünya'nın bir yerinde kısa bir süre için görülebilecekleri anlamına geliyor. Gelgit hareketlerinin bir sonucu olarak, Ay Dünya'dan uzaklaşıyor - 260 milyon yıl sonra o kadar uzakta olacak ki biz (biz???) sadece halka şeklindeki tutulmaları göreceğiz.
Görünüşe göre ilk tahmin eden duraklama, Miletli Thales'ti (MÖ 28-585 yüzyıllar). Muhtemelen bunun gerçekten olup olmadığını, yani tahmin edip etmediğini bilemeyeceğiz, çünkü Küçük Asya'daki tutulmanın MÖ 567, 566 M.Ö. Tabii ki, bugünün zaman hesabı için verileri alıntılıyorum. Çocukken, insanların yılları nasıl saydığını hayal ederdim. Yani bu, örneğin, MÖ XNUMX, Yılbaşı Gecesi geliyor ve insanlar seviniyor: MÖ sadece XNUMX yıl! Sonunda “bizim çağımız” geldiğinde ne kadar mutlu olmuş olmalılar! Birkaç yıl önce yaşadığımız nasıl bir bin yıl dönümü!
Tarihleri ve Aralıkları Hesaplamanın Matematiği tutulmalar, özellikle karmaşık değildir, ancak düzenlilik ve daha da kötüsü, vücudun yörüngelerdeki düzensiz hareketi ile ilgili her türlü faktörle doludur. Hatta bu matematiği bilmek istiyorum. Thales of Milet nasıl gerekli hesaplamaları yapabilirdi? Cevap basit. Bir gökyüzü haritanız olmalı. Böyle bir harita nasıl yapılır? Bu da zor değil, eski Mısırlılar nasıl yapılacağını biliyorlardı. Gece yarısı iki rahip tapınağın çatısına çıkar. Her biri oturur ve gördüğünü çizer (meslektaşı gibi). İki bin yıl sonra gezegenlerin hareketi hakkında her şeyi biliyoruz ...
Güzel geometri veya "halı" üzerinde eğlence
Yunanlılar sayıları sevmediler, geometriye başvurdular. Yapacağımız şey bu. Bizim duraklama basit, renkli ama bir o kadar da ilginç ve gerçek olacaklar. Mavi figürün kırmızı figürü gölgede bırakacak şekilde hareket ettiği geleneğini kabul ediyoruz. Mavi şekle ay, kırmızı şekle güneş diyelim. Kendimize şu soruları soruyoruz:
- bir tutulma ne kadar sürer;
- hedefin yarısı kapatıldığında;
Pirinç. 1 Güneş ve ay ile çok renkli "halı"
- maksimum kapsama alanı nedir;
- Kalkan kapsamının zamana bağımlılığını analiz etmek mümkün mü? Bu yazıda (metin miktarıyla sınırlıyım) ikinci soruya odaklanacağım. Bunun arkasında güzel bir geometri var, belki de sıkıcı hesaplamalar olmadan. Figür'e bakalım. 1. Bir güneş tutulması ile ilişkilendirileceği varsayılabilir mi?
Dürüstçe söylemeliyim ki, tartışacağım görevler ortaokul ve lise öğrencilerinin bilgi ve becerilerine göre özel olarak seçilecektir. Ancak müzisyenlerin terazi çalması ve sporcuların genel gelişim egzersizleri yapması gibi görevler üzerinde çalışıyoruz. Ayrıca çok güzel bir halı değil mi (şekil 1)?
Pirinç. 2 "Mavi" Ay ve "Kırmızı" Güneş
Gök cisimlerimiz, en azından başlangıçta, renkli kareler olacaktır. Ay mavi, güneş kırmızı (renklendirme için en iyisi). şimdiki zamanla duraklama Ay gökyüzünde güneşi kovalar, yakalar ... ve onu kapatır. Bizde de aynısı olacak. En basit durum, Şekil 2'de gösterildiği gibi Ay'ın Güneş'e göre hareket etmesidir. 2. Tutulma, Ay diskinin kenarı Güneş diskinin kenarına değdiğinde başlar (Şekil XNUMX) ve onun ötesine geçtiğinde sona erer.
Pirinç. 3 Ay güneşe çapraz olarak yaklaşıyor
"Ay"ın birim zaman başına, örneğin dakikada bir hücre hareket ettiğini varsayıyoruz. Tutulma daha sonra sekiz birim, diyelim dakika sürer. Yarım güneş tutulmaları tamamen karartılmış Kadranın yarısı iki kez kapatılır: 2 ve 6 dakika sonra. Yüzde karartma grafiği basittir. İlk iki dakika boyunca, kalkan sıfıra 1 oranında eşit olarak kapanır, sonraki iki dakika aynı oranda açığa çıkar.
İşte daha ilginç bir örnek (Şekil 3). Ay güneşe çapraz olarak yaklaşır. Dakika başı ödeme anlaşmamıza göre tutulma 8√2 dakika - bu sürenin ortasında tam bir güneş tutulması yaşıyoruz. t zamanından sonra güneşin hangi kısmının kaplandığını hesaplayalım (Şek. 3). Tutulmanın başlangıcından bu yana t dakika geçtiyse ve sonuç olarak Ay Şekil 5'deki gibidir. 4, sonra (dikkat!) Bu nedenle, güneş diskinin yarısı kadar kaplanmıştır (APQR karesinin alanı), bu nedenle, yani ne zaman kaplanmıştır? 4 dakika sonra (daha sonra tutulmanın bitiminden XNUMX dakika önce).
Pirinç. 4 "Gölgeleme" fonksiyonunun grafiği
bütünlük bir an sürer (t = 4√2) ve "gölgeli kısım" fonksiyonunun grafiği iki parabol yayından oluşur (Şekil 4).
Mavi ayımız kırmızı güneş ile köşeye değecek, ancak çapraz olarak değil, biraz çapraz olarak onu kaplayacak.Hareketi biraz karmaşıklaştırdığımızda ilginç bir geometri ortaya çıkıyor (Şekil 6). Hareket yönü şimdi vektör [4,3], yani "dört hücre sağa, üç hücre yukarı". Güneş'in konumu öyledir ki, "gök cisimlerinin" kenarları uzunluklarının dörtte birine yakınsadığında tutulma başlar (A konumu). Ay B konumuna geçtiğinde Güneş'in altıda birini, C konumunda ise yarısını tutacaktır. D konumunda tam bir tutulma var ve sonra her şey "olduğu gibi" geri dönüyor.
Pirinç. 5 Güneş'in t zamanında gizlenmiş parçası
Ay G konumundayken tutulma sona erer. bölüm uzunluğu AG. Daha önce olduğu gibi, Ay'ın "bir kare" geçtiği süreyi bir zaman birimi olarak alırsak, AG'nin uzunluğu eşittir. Gök cisimlerimizin 4'e 4 olduğu eski görüşüne geri dönersek, sonuç farklı olurdu (ne?). Gösterilmesi kolay olduğu gibi, hedef t < 15'ten sonra kapanır. “Ekran kapsama yüzdesi” fonksiyonunun grafiği şekil 6'de görülebilir. XNUMX.
Pirinç. 6 "Yüzde koruma" işlevinin grafiği
Tutulma ve atlama denklemi
Pirinç. 7 Şekilde gösterilen tutulma sırasında güneş diskinin tıkanması. 6
Çemberler örneğini dikkate almasaydık, tutulmalar sorunu eksik kalırdı. Bu çok daha karmaşıktır, ancak bir dairenin diğerinin yarısını ne zaman gölgede bıraktığını - ve en basit durumda, bunlardan birinin ikisini birbirine bağlayan çap boyunca hareket ettiğini anlamaya çalışalım. Çizim, bazı kredi kartı sahiplerine tanıdık geliyor.
Alanların konumunu hesaplamak karmaşıktır, çünkü ilk olarak, dairesel bir segmentin alanı için formül bilgisi, ikincisi, açının yayı bilgisi ve üçüncüsü (ve hepsinden kötüsü), yetenek gerektirir. belirli bir atlama denklemini çözmek için. "Geçişli denklem"in ne olduğunu açıklamayacağım, bir örneğe bakalım (Şekil 8).
Pirinç. 8 "Küresel" tutulma
Dairesel bir bölüm, düz bir çizgi ile bir daire kestikten sonra kalan "kase" dir. Böyle bir segmentin alanı S = 1/2r'dir.2(φ-sinφ), burada r dairenin yarıçapıdır ve φ, parçanın üzerinde durduğu merkezi açıdır (Şekil 8). Bu, üçgenin alanını dairesel sektör alanından çıkararak kolayca elde edilir.
Bölüm O1O2 (dairelerin merkezleri arasındaki mesafe) daha sonra 2rcosφ/2'ye eşittir ve yükseklik (genişlik, “bel çizgisi”) h = 2rsinφ/2'dir. Bu nedenle, Ay'ın güneş diskinin yarısını ne zaman kaplayacağını hesaplamak istiyorsak, denklemi çözmemiz gerekir: bu, sadeleştirmeden sonra şöyle olur:
Pirinç. 9 İki fonksiyonun grafiği
Bu tür denklemlerin çözümü basit cebirin ötesine geçer - denklem hem açıları hem de trigonometrik fonksiyonlarını içerir. Denklem, geleneksel yöntemlerin erişiminin ötesindedir. Bu yüzden denir zıplamak. Önce her iki fonksiyonun yani fonksiyonların ve fonksiyonların grafiklerine bakalım.Bu şekilden yaklaşık bir çözüm okuyabiliriz. Ancak, yinelemeli bir yaklaşım elde edebiliriz veya… Excel elektronik tablosundaki Çözücü seçeneğini kullanabiliriz. 20. yüzyıl olduğu için her lise öğrencisi bunu yapabilmelidir. Daha karmaşık bir Mathematica aracı kullandım ve işte XNUMX ondalık gereksiz hassasiyetteki çözümümüz:
Kesinliği Belirle[FindRoot[x==Sin[x]+Pi/2,{x,2}],20] {x⇒2.3098814600100574523}.
Pirinç. 10 matematica'da tutulma animasyonu
Bunu 180/π ile çarparak dereceye çeviriyoruz. 132 derece, 20 dakika, 45 ve bir yay saniyenin çeyreği elde ediyoruz. Çemberin merkezine olan uzaklığın O olduğunu hesaplıyoruz.1O2 = 0,808 yarıçap ve "bel" 2,310.

